What is Computational Fluid Dynamics?
Fluid dynamics is concerned with the motion of fluids (liquids and gases) and the forces on them. “Computational” refers to computation of the flow and forces using numerical analysis. A literal definition of “ computational fluid dynamics ” might therefore be “the prediction of fluid motion and forces by computation using numerical analysis”. However, the term has been adopted to describe a broader range of calculations for numerous scientific and engineering applications. Notably, it is used in many applications involving heat, including the following:
- engines, e.g turbines, internal combustion engines;
- heat recovery, e.g. heat exchangers;
- thermal management, e.g. electronics cooling, automotive exhaust systems;
- thermal comfort, e.g. heating, ventilation, and air conditioning.
Thermodynamics is an important aspect of many of these applications. Some applications involve combustion or, more broadly, chemistry. Heat transfer computations can include solid materials; likewise can chemistry calculations.
A modern definition of “ computational fluid dynamics ” might therefore be “the prediction of fluid motion and forces by computation using numerical analysis, generally extended to include heat, thermodynamics, chemistry and solids”.
Motion and Forces
Computational fluid dynamics (CFD) involves the solution of partial differential equations (PDEs), principally the conservation laws of mass and linear momentum that govern fluid motion and forces. Closed-form solutions of these PDEs exist only for very simple geometries and flow regimes, e.g. the Hagen-Poiseuille equation for laminar flow of an incompressible, Newtonian fluid in a long pipe of constant cross section. For real world problems, e.g. turbulent flow around a complex geometry such as a car, engineers use CFD to calculate flow velocities and pressures to predict aerodynamic performance, e.g. lift and drag forces. They visualise the flow with streamlines, cutting planes, boundary surfaces, etc (see image).
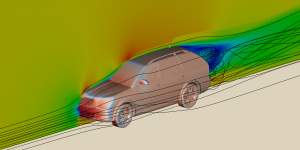
Numerical Analysis
CFD uses numerical methods that represent each PDE as a set of algebraic equations at discrete points in the solution domain; the algebraic equations are solved by the inclusion of suitable boundary conditions. The finite volume method is a popular numerical method which subdivides the solution domain into a mesh of small volumes, or cells. Each cell includes discrete values, e.g. for velocity, typically at its centre. The system of linear equations, e.g. for velocity, produces a sparse matrix that is usually solved using iterative methods. The finite volume method is popular because it lends itself to iterative solution of complex sets of equations and parallel computing by domain decomposition.
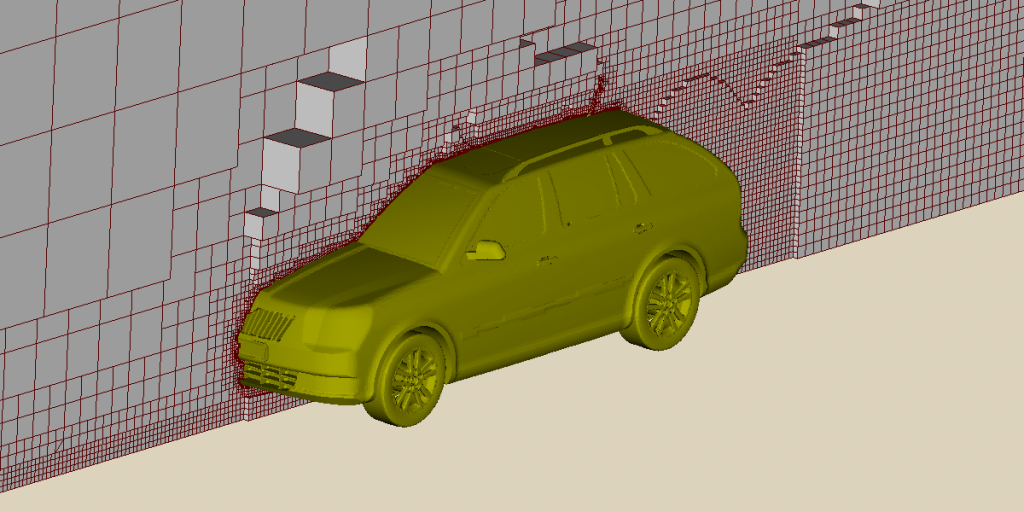

Heat and Thermodynamics
For applications involving heat, solutions include a PDE for the conservation of energy. The equation can include thermal conduction, convection and sources including thermal radiation and chemical reactions. Thermodynamics relates internal energy to temperature, which affects the flow of heat. Heat transfer may involve conducting solid materials coupled with fluid flow, known as conjugate heat transfer.
Particle Methods
Many engineering applications include particles of liquid or solid. Liquid sprays are particularly common, e.g. for cooling, coating, cleaning, agriculture, food production, fire suppression, emission reduction and fuel injection. Solid particles exist in applications such as filtration, erosion, and fluidised beds. Many CFD software packages include methods to represent particles, with properties such as size, composition, speed, temperature, etc. Tracking methods predict the particle positions and can include collision modelling. The software generally couples the particles and bulk fluid flow so that the flow transports the particles with it, with models for drag force, dispersion, etc. Particles may include further models with coupling to the bulk fluid, including heat transfer, thermodynamics, reactions and phase change.
Chemistry
Some CFD applications include predictions of heat generation by combustion. Combustion chemistry and chemical kinetics is complex and there are many combustion models for CFD that make approximations to lower the calculation cost. The approximations relate to assumptions about the combustion, e.g. the level of turbulence and mixing of fuel and oxidant. Many CFD solvers evolve the concentration of chemical species, e.g. methane and oxygen, within the flow. They define reactions between the species by a set ordinary differential equations (ODEs) as a function of time. Solution of the ODEs uses additional methods of numerical analysis.
