OpenFOAM is software for computational fluid dynamics with a strong reputation for multiphase flows. It includes several solvers that capture interfaces between liquid-gas phases (e.g. water-air) based on the volume of fluid (VoF) method. The method solves transport equations for one or more phase fractions “α” (0 ≤ α ≤ 1), where the surface at α = 0.5 describes the interface. Spanning a period of 20+ years, Henry Weller of CFD Direct made VoF in OpenFOAM robust, usable and efficient by key innovations, including:
- the MULES algorithm — semi-implicit and second order in time — to ensure α remains between strict bounds of 0 and 1;
- the interface compression scheme, based on counter-gradient transport, to maintain sharp interfaces during a simulation.
Users have adopted this industrial-strength methodology for small scale flows in mechanical and medical engineering. It works for intermediate scales in process engineering and for the largest scales of civil engineering hydraulics and marine hydrodynamics.
Interpolation for interface capturing
In July 2020, CFD Direct released a framework for surface interpolation in interface capturing in the public, development line of OpenFOAM (OpenFOAM-dev). All interpolation schemes, used for flux calculation in advection, operate with the existing MULES-based solvers, e.g. interFoam. They are inherently robust with bounded, conservative numerics that can operate 2nd-order in time and efficiently with large time steps. The redesign of flux interpolation is extensible to new schemes. There is improved usability with a simple selection of interpolation scheme in the fvSchemes file, e.g. the standard interface compression with vanLeer interpolation:
div(phi,alpha) Gauss interfaceCompression vanLeer 1;
Piecewise-linear interface calculation (PLIC)
To accompany the new framework, we developed a new family of interpolation schemes based on piecewise-linear interface calculation (PLIC). PLIC represents an interface by surface-cuts which split each cell to match the volume fraction of the phase in that cell. The surface-cuts are oriented according to the point field of the local phase fraction. The phase fraction on each cell face — the interpolated value — is then calculated from the amount submerged below the surface-cut.
The basic PLIC method generates a single cut so cannot handle cells in which there are multiple interfaces or where the interface is not fully resolved. In those cells, the interpolation reverts to an alternative scheme, typically standard interface compression. PLIC, with a fallback to interface compression, produces robust solutions for real engineering cases. It can run with large time steps so can solve problems like hydrodynamics of a planing hull, with rigid body motion of the hull (above). The user selects PLIC by the following setting in fvSchemes.
div(phi,alpha) Gauss PLIC interfaceCompression vanLeer 1;
Multicut PLIC (MPLIC)
A separate multicut PLIC (MPLIC) scheme extends PLIC to handle multiple surface-cuts. Where a single cut is insufficient, MPLIC performs a topological face-edge-face walk to produce multiple splits of a cell. If that is still insufficient, MPLIC decomposes the cell into tetrahedrons on which the cuts are applied. The extra cutting carries an additional computational cost but requires no fallback. The user selects MPLIC by the following setting in the fvSchemes file:
div(phi,alpha) Gauss MPLIC;
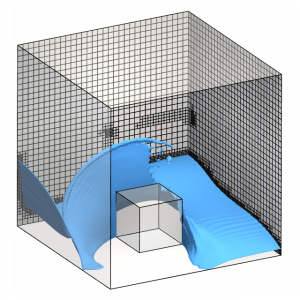
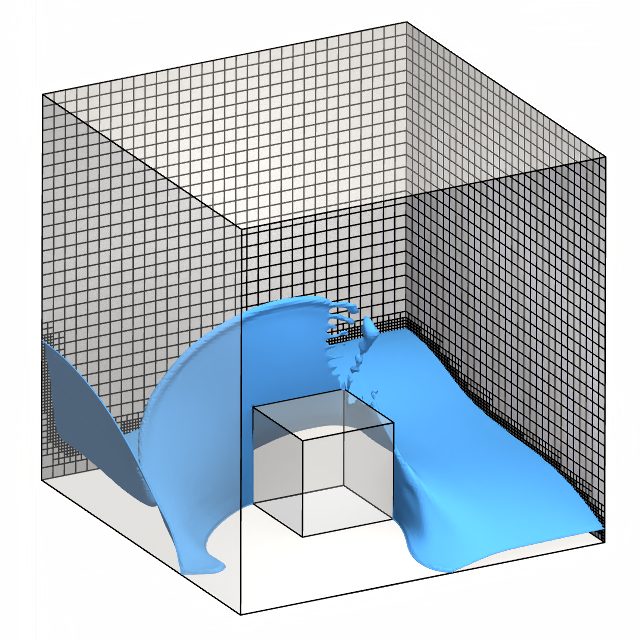
Refinement patterns
The PLIC and MPLIC methods are more precise than interface compression for meshes with refinement patterns. With interface compression, the damBreakWithObstacle example above reveals numerical oscillations of the interface, due to dynamic mesh refinement. With (M)PLIC, the oscillations disappear. Interface oscillations also occur for the planing hull when the mesh includes refinement patterns. The oscillations causes excessive entrainment of air beneath the hull, leading to an inaccurate prediction of forces on the hull. (M)PLIC reduces these oscillations for a better prediction of the forces.
High shear
Variants of the PLIC and MPLIC schemes are also available which use velocities at the face points to calculate the face flux. These PLICU and MPLICU schemes are likely to be more accurate in regions of interface under high shear force.